Here, for the record, are some technical papers I wrote in college and shortly thereafter.
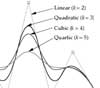
An Introduction To Knot Vectors A tutorial on B-Spline curves, and in particular, on how to use the knot vector to control their shape. (PDF, 104K)
Arc Length Parametrization of Spline Curves. A useful mathematical exercise: How to use Chebyshev polynomials to create spline curves with arc-length parametrization (PDF, 226K)
The Utah Raster Toolkit Image processing in the days before Photoshop. Later made popular by Craig Kolb’s Rayshade (PDF, 1.4MB)
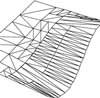
Ray Tracing Spline Surfaces with Motion Blur A distillation of my MS thesis, it describes how to efficiently ray trace spline surfaces. Some of the techniques, such as the “pixel thresher” are still interesting. (PDF, 328K)
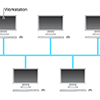
Distributed Computation for Computer Animation A survey of techniques for lashing together Unix workstations to compute animated movie frames. (PDF, 187K)
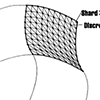
Tessellation of NURB Surfaces Originally published in Graphics Gems IV, 1994. As of this writing it’s still in print (and I get a whopping $0.07 for each copy sold!).
A great tutorial on how to turn surfaces into triangles for rendering or computation. (Amazon
Patents
More recent research efforts have been consumed by lawyers, further obfuscated, and fed to the US Patent office (a side effect of corporate patent filing bonuses). Out of thirty-odd patents, here are a few of the more interesting ones:
5,428,718: Tessellation System – Some interesting tricks for speeding up B-Spline surface tessellation (w/Shaun Ho)
6,911,980: Manipulation of Curves and Surfaces – Direct manipulation UI techniques for 2D warping (w/Martin Newell)
7,006,707: Projecting Images Onto a Surface – Re-constructing camera parameters from a perspective-warped frame
7,385,612: Distortion of Raster and Vector Artwork – Applying the same Bezier warp to both vector and raster artwork simultaneously
8,378,781: Animated Light String System – Synchronized animations on a string of lights over a single daisy-chained serial line
11,069,028: Automated Generation of Anamorphic Images for Catoptric Anamorphosis – Automatically generate distorted images that look correct when viewed reflected in a cylinder