CAD & 3D Printing
Category Archives: 3D
Some Boots for the Lelo Self-Balancing Triangle
May 15, 2024 – 9:22 pm
One of the cool things modern tech has made straightforward is the ability for gadgets to balance themselves. Spinning reaction wheels allow a device to change its position and hold it in place, even if it’s balancing on a point. Last century, this would have been a major (and expensive!) engineering challenge. Today inexpensive nano-tech gyroscopes, direct-drive motors and microcontrollers have reduced automatic balancing to an engineering class project.
I’d love to learn more about this and build such a device. Check out this YouTube channel for a whole variety of homemade balancing devices. In the mean time, you can buy a fun demo from Nikolatoy: The Lelo self-balancing triangle. This is a commercial version of an open-source project that apparently is very popular in China (YouTuber RemRC’s version is here).
One of the clever tricks Nikolatoy used to reduce the cost of their triangle was to make the frame out of the circuit boards. Unfortunately, the edges of the boards have poor traction, and it’s difficult for the triangle to balance itself without getting stuck slipping back and forth.
I solved this by creating a set of “boots” to put around the edge of the boards, giving the triangle a lot more grip.
This dramatically improves the ability of triangle to function (see the video below). I’ve posted the STLs if you want to print your own, using a soft, flexible material such as TPU. Or, (shameless plug!) you can simply buy a set of them from me on Shapeways (remember to order two of them). [Sadly, as of July 2024, Shapeways.com has gone out of business. You can find other venders by googling “TPU 3D printing services”]
The Fit Testing Block
December 28, 2019 – 12:49 pm
How Accurate is Your 3D Print?
I Tested Several Services to Find Out
Update September 2024: Several of the entries in this post referred to services (e.g., Shapeways) that are no longer in business, or 3D printing tech that is now obsolete. I’ve archived these old reviews elsewhere, but removed them from this post for brevity. Even though Shapeways is no longer around, I left the story about their process variations as a useful story of what can happen even with a particular process at a specific vendor. This post has been updated with reviews of several contemporary services.
Decades ago, if you wanted to create your own printed circuit board, you had to make it yourself. This was quite involved – you bought a copper plated blank board, created the circuit patterns on it with resist (tape, rub-on patterns, or Sharpie), then dunked it in noxious chemicals to etch the unmarked copper away. It was also up to you to drill the holes. Then you tracked down problems because too much (or not enough) copper was dissolved, opening or shorting your circuits. It was messy, tedious and frustrating.
Here in the future, all those problems are solved. You design the board in a CAD program, then the Internet whisks the design to a far-off fabrication house. A few weeks later your boards arrive, perfectly manufactured with solder masks, silk-screen markings, plated through holes – things you’ll never get making them at home.
I do some amount of 3D printing, but I have no desire to own a 3D printer. Running your own 3D printer still feels like those early days of homemade circuit boards. The tedious details of bed leveling and heating, getting the model to stick in place, support sprues, filament moisture content, speed settings all have to be carefully looked after to get good results. I prefer the modern circuit board model for 3D prints – send the model off to a factory with equipment and materials you’ll never afford, and get your polished results back in the mail.
When I started ordering 3D prints, I had a basic question: when designing two parts that fit together, how much space do you need to leave between them to fit properly? To research this, I designed a set of fit-testing sets and printed them with various processes to see what sort of tolerances are necessary. So far I’ve tried nine different prints, and (unlike circuit boards) the results vary considerably.
The fit testing sets consist of two parts, a pair of pegs, each with round and square ends. One peg has 5mm ends, the other is 10mm. The other component is a block with a range of holes of different sizes to test fit each peg. Printing these and testing which hole each peg fits in helps to determine how much extra margin your design needs to have parts fit together well. For example, if the peg fits comfortably in the +0.2mm hole, that means you’d better leave a 0.2mm gap in your design for the parts to work smoothly.
The first blocks I made ranged from -9.85 to 10.15 (in increments of 0.05mm) for the large holes, and -4.875 to 5.125 (with 0.025mm steps) for the small ones. I quickly discovered this wasn’t enough range for coarser printing processes, so I created additional blocks with wider ranges of 9.7 to 10.3 (9.75 to 10.25) and 0 to 0.6 (0 to 0.5). These doubled the increment steps of the previous blocks, from 0.05 / 0.025 mm to 0.1 / 0.05.
The last block works well for the coarsest printing technologies, and is the best place to start for basic FDM (fused deposition modelling) printers. The rendering above also shows some quarter-step peg sets I modeled for even more precise tests, but you won’t need those anywhere outside of a Swiss watch factory.
Over the past few years I’ve printed blocks and pegs with a number of different services, to get a feel for the accuracy and tolerances of each. Read on for a review of what I discovered.
read moreDesign Lesson Learned: Model the Environment
September 5, 2019 – 1:26 pm
On a recent trip I picked up a art-glass marble for my wife. She liked it so much she bought a nice lighted display stand for it. The stand wasn’t designed to display that particular marble though, so it didn’t work too well.
This was a problem easily solved with a bit of 3D printing. I figured it’d be trivial to make an adapter ring for the marble to sit securely on. However, when I examined the stand, I discovered the LEDs were flush with the base, and likely to get in the way. The marble needed to be held up above them. Before starting on the adapter, I did a simple model of the stand, so I could check everything cleared.
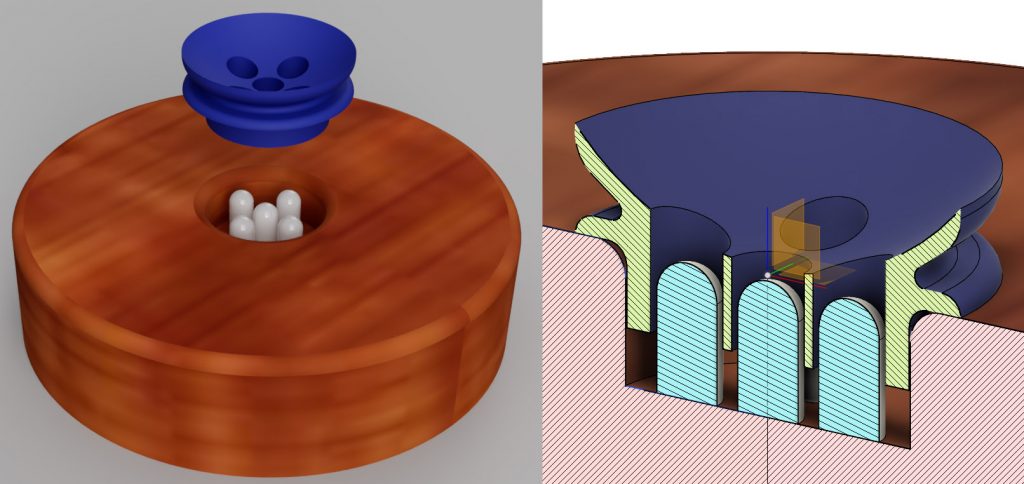
With the stand and LEDs modeled, I could verify my design properly fit. The project worked great, and fit perfectly with the first print. Success.
The next CAD project I did was a stand for a screwdriver set I purchased. I carefully measured the handle and the various blades, but (perhaps over-confident) didn’t bother to model them.
It wasn’t until I got the print back I discovered a major ergonomic fail: You can’t easily reach the handle because the blades are in the way! Had I taken the time to actually model the blades and handle, I would have visualized this immediately, and chosen another layout.
Moral – it’s a good idea to model the whole environment, not just the piece you’re printing.
How to Make Apple’s Mac Pro Holes
June 16, 2019 – 11:15 am
Apple’s recently introduced Mac Pro features a distinctive pattern of holes on the front grill. I’m not likely to own one anytime soon (prices for a well configured machine approach a new car), but that pattern is very appealing, and re-creating it is a fun exercise.
The best clue about the pattern comes from this page pitching the product. About halfway down, by the heading “More air than metal” is a short video clip showing how the hemispherical holes are milled to create the pattern.
Let’s start with a screen grab of the holes from the front. The holes are laid out with their centers equally spaced apart and the tops of the lower circles fall on the same line as the bottom of the circles above them. So the circles are spaced 2r apart vertically, where r is the radius of the circle.
The horizontal spacing is a bit more work. The angles of the equilateral triangle formed by the centers are 180°/3 = 60° (or π/3 as they say in the ‘hood). If you draw a vertical line from the center of the top circle to the line connecting the centers of the bottom circles, that line (as you see above) is 2r long. With a bit of trig, you can find half the horizontal spacing x by using the right triangle formed by that line, x and the side of the equilateral triangle. The angle from the vertical center line to the equilateral triangle edge is half of π/3, π/6. So,
\[x=2r\tan \frac{\pi }{6}\]and 2x is the horizontal spacing of the circles.
The hemispherical holes are milled into both sides of the plate, but the holes on the other side are offset so the hole centers on one side fall exactly in the middle of the triangle formed by the hole centers on the other side:
You already know the horizontal offset for the centers from one side to the other is x, but how far up do you go to hit the center of that triangle? Let’s call that h.
You’ll use the same tan(π/6) trick we used above, this time using the triangle formed by x and h. Like the triangle used to find x, the angle here is also π/6. So:
\[h=x\tan \frac{\pi }{6}\]Let’s clean this up a bit:
\[h=x\tan \frac{\pi }{6}=2r\tan \frac{\pi }{6}\tan \frac{\pi }{6}\]
\[\tan \frac{\pi }{6}=\frac{1}{\sqrt{3}}\] so…
\[h=2r\frac{1}{\sqrt{3}}\frac{1}{\sqrt{3}}=\frac{2r}{3}\]
There’s still the issue of how thick the plate is, relative to the size of the holes. I took screen grabs of the film clip and compared them by counting pixels:
Examining the images, the thickness was about 101, with the diameter (2r) of the holes coming in at 176. Now, these numbers aren’t at all precise, because of the perspective introduced by whatever animation software was used. But I can’t help but notice the following coincidence:
\[ \frac{101}{176}=0.573\approx \tan \frac{\pi }{6}=\frac{1}{\sqrt{3}}=0.577\]Yeah. The ratio of the plate thickness to the hole diameter is just like the ratio of the hole horizontal spacing to the hole diameter. So let’s turn this around, and summarize by saying for a plate of any thickness t, use:
\[r=\frac{t\sqrt{3}}{2}\]
\[x=2r\tan \frac{\pi }{6}=\frac{2r}{\sqrt{3}}=t\]
\[h=\frac{2r}{3}\]
Where r is the radius (half the diameter) of the spheres and 2x is the horizontal spacing of the sphere centers on a given row. For the next row, the centers are offset by x horizontally from the centers of the previous row. The rows are spaced 2r apart vertically, from sphere center to center. The same grid of spheres carved into the back side is displaced by x horizontally, and h vertically from the spheres in the front. The centers of the front spheres are on the front surface of the plate, the back spheres on the back.
So to CAD this up, all you need to do is start with a rectangular block of thickness t, and use the formulas above to place the centers of the spheres (with diameter 2r) on the front and back of the block.
If you just want to quickly print or look at the result in 3D, I’ve posted some sample STL files on Thingiverse.
The Three Piece Burr Puzzle
June 23, 2018 – 12:10 pm
Somewhere around middle-school, I came across a diagram of the classic three-piece burr puzzle.
It looked fun, so I endeavored to make one. Unfortunately, the materials available to me then (a scrap of plywood and a janky power scroll saw) didn’t produce very good results. It worked, but was crude and wobbly. Spray painting it black didn’t help.
A couple years ago, I revisited the project, this time with 3D printing.
Printed at Shapeways in dyed plastic, it works great. It’s kind of pricey though, running just over $90 for the three solid pieces. Similar puzzles retail for less than $5. I tried making hollow versions to lower the price, but it reduced it less than 20%, and required annoying holes to drain the trapped material.
Yes, I could just have bought one. But there’s something fun about precisely realizing something you envisioned decades ago.
Update Feb 2022
I recently printed the burr puzzle in bronze/gold/nickel plated steel from Shapeways. I shrunk the puzzle to half size to keep the cost reasonable, but did not adjust the model to account for the difference in the material tolerance. It took a fair amount of filing on the interior slots to get the pieces to fit properly.
The Raspberry Cup and Saucer
February 10, 2018 – 12:53 pm
My mom collects teacups, and I liked the idea of creating one using 3D tech. She also grows raspberries in her garden – eating them off the vines is always a treat when we visit in the summer. I was mulling over ideas for a raspberry teacup design when the idea struck of using a raspberry leaf as the saucer. Then I started in earnest. This is perhaps an afternoon project for an experienced ceramics artist. But I’m more fond of CAD then wet clay, so I designed it in Fusion 360, and had it fabricated with Shapeway’s porcelain process.
3D: Replacement Stove Knobs
October 17, 2016 – 9:55 am
We have an aging Thermador gas range. One of the original plastic knobs broke. Surprisingly, it was hard to find replacements. Thermador no longer supplied them, and the 6mm D-shaft was an unusual size for generic replacements. The closest I could come was some generic knobs off ebay. But these didn’t have the proper stop inside the sleeve, so you couldn’t push the shaft in before turning it (a safety feature of the Thermador knobs). I kludged some stops with chopstick pieces, but it was clumsy. Time to roll our own. read more
